Rekürsif fonksiyonlar, kendini çağıran fonksiyonlardır. Bir problemi daha küçük alt problemlere bölerek çözmek için kullanılırlar. Matematiksel işlemler, veri yapıları ve algoritmalar gibi birçok alanda kullanılırlar.
1. Rekürsif Fonksiyonun Mantığı
Rekürsif bir fonksiyon, en az bir temel duruma (base case) ve en az bir rekürsif çağrıya (recursive call) sahip olmalıdır:
- Temel Durum (Base Case): Fonksiyonun sonlanmasını sağlar. Eğer temel durum olmazsa fonksiyon sonsuz döngüye girer.
- Rekürsif Durum: Fonksiyon kendisini çağırarak problemi daha küçük bir hale getirir.
2. Rekürsif Fonksiyon Örneği: Faktöriyel Hesaplama
Faktöriyel (n!) matematiksel olarak şu şekilde tanımlanır:
n!=n×(n−1)!
1 != 1, 0!=1
Bunu rekürsif fonksiyon olarak yazalım:
#include <iostream>
using namespace std;
int Faktoriyel(int n) {
if (n <= 1) // Temel durum
return 1;
return n * Faktoriyel(n - 1); // Rekürsif çağrı
}
int main() {
int sayi = 5;
cout << sayi << "! = " << Faktoriyel(sayi) << endl;
return 0;
}
Çıktı:
5! = 120
3. Fibonacci Serisi Rekürsif Fonksiyon ile Hesaplama
Fibonacci serisi şu şekilde tanımlanır:
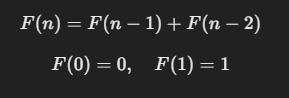
Kod:
#include <iostream>
using namespace std;
int Fibonacci(int n) {
if (n == 0) return 0; // Temel durum
if (n == 1) return 1; // Temel durum
return Fibonacci(n - 1) + Fibonacci(n - 2); // Rekürsif çağrı
}
int main() {
int sayi = 7;
cout << sayi << ". Fibonacci sayısı: " << Fibonacci(sayi) << endl;
return 0;
}
Çıktı:
7. Fibonacci sayısı: 13
4. Rekürsif Fonksiyon ile Sayıların Toplamı
Verilen n sayısına kadar olan sayıların toplamını hesaplayan bir rekürsif fonksiyon yazalım:
Toplam(n)=n+Toplam(n−1)
Toplam(1)=1
#include <iostream>
using namespace std;
int Toplam(int n) {
if (n == 1) // Temel durum
return 1;
return n + Toplam(n - 1); // Rekürsif çağrı
}
int main() {
int sayi = 10;
cout << "1'den " << sayi << "'e kadar olan sayıların toplamı: " << Toplam(sayi) << endl;
return 0;
}
Çıktı:
1'den 10'e kadar olan sayıların toplamı: 55
5. Rekürsif Fonksiyon ile Sayının Basamak Sayısını Bulma
Bir sayının kaç basamaklı olduğunu bulan rekürsif fonksiyonu yazalım:
#include <iostream>
using namespace std;
int BasamakSayisi(int n) {
if (n < 10) // Temel durum: Tek basamaklıysa 1 döndür
return 1;
return 1 + BasamakSayisi(n / 10); // Sayıyı küçülterek devam et
}
int main() {
int sayi = 12345;
cout << sayi << " sayısı " << BasamakSayisi(sayi) << " basamaklıdır." << endl;
return 0;
}
Çıktı:
12345 sayısı 5 basamaklıdır.
6. Rekürsif Fonksiyon ile Sayının Tersini Bulma
Bir sayıyı tersine çeviren rekürsif fonksiyonu yazalım:
#include <iostream>
using namespace std;
void SayiyiTersCevir(int n) {
if (n == 0) return; // Temel durum
cout << (n % 10); // Son basamağı yazdır
SayiyiTersCevir(n / 10); // Kalan sayıyı fonksiyona gönder
}
int main() {
int sayi = 1234;
cout << sayi << " sayısının tersi: ";
SayiyiTersCevir(sayi);
cout << endl;
return 0;
}
Çıktı:
1234 sayısının tersi: 4321
7. Rekürsif Fonksiyon ile Üs Alma (Power Function)
#include <iostream>
using namespace std;
int UsAl(int taban, int us) {
if (us == 0) return 1; // Temel durum
return taban * UsAl(taban, us - 1); // Rekürsif çağrı
}
int main() {
int taban = 2, us = 5;
cout << taban << "^" << us << " = " << UsAl(taban, us) << endl;
return 0;
}
Çıktı:
2^5 = 32
Sonuç
Rekürsif fonksiyonlar, problemlerin küçük alt problemlere bölünerek çözülmesine yardımcı olur. Ancak, her rekürsif çağrı bellekte yer kapladığı için fazla kullanımı performans sorunlarına yol açabilir. Bu yüzden, iteratif (döngü tabanlı) çözümler ile karşılaştırılmalı ve en uygun yöntem seçilmelidir.



